Home Transit of Venus Sewer History in Leeds Sundials in Leeds William Gascoigne John Feild About

Part 4 - The First Observations of Transits

Kepler correctly predicted that an ascending node transit of Venus would occur in December 1631, but no-one observed it - due to the fact that it occurred after sunset for most of Europe. Kepler himself died in 1630. He not only predicted this particular transit but also worked out that transits of Venus involve a cyclical period of approximately 120 years.

The first ever transit of a planet - Mercury (also predicted by Kepler) - had been observed by Pierre Gassendi in Paris in the previous month. The observation of transits was only possible using a telescope - an instrument only popularised for astronomy around 1610, by Galileo Galilei (1564-1642). Transits therefore were a celestial phenomenon whose time had come!

Jeremiah Horrocks (born c.1619) was fortunate enough to own a small telescope: probably a 1½" galilean (refracting) telescope. He only lived to the age of 22, but in his short life he blazed a trail for modern astronomy in England. He was convinced by his own observations that available tables for planetary positions were incorrect and he resolved to gather new data rather than to try to modify old tables. He had read many of the recent continental astronomical texts and accepted Kepler's theories relating to elliptical orbits. Horrock's place in astronomical history was secured when he managed to predict that a further transit of Venus would occur on 4th December 1639 (24th November 1639, Old Style), 8 years after the one predicted by Kepler and much earlier than the 120 year wait predicted by Kepler.

The predicted day of transit was a Sunday. Horrocks was set up to observe the transit from his room in Hoole (near Liverpool). The method he used involved projecting the image of the Sun from his telescope onto a graduated sheet of paper in such a way that the image filled a six-inch diameter circle. The horizontal diameter of the circle was divided into 30 equal parts and it was in terms of these parts, rather than in any standard units or angles, that Horrocks recorded his measurements.

He kept an almost unbroken watch from 9am until noon and made intermittent observations between noon and 1pm. He was otherwise engaged between 1pm and 3.15pm by "business of the highest importance which, for these ornamental pursuits, I could not with propriety neglect". These words lie behind the well-established tradition that Horrocks was a clergyman.

By the time he returned to his observing, he found that the transit had already begun. He was astonished by how small Venus appeared: a small black circle which had already entered fully onto the face of the Sun.

A plumb line was suspended in such a way that it cast a vertical shadow on the centre of the Sun's image, as an aid to measurement.

Horrocks made measurements at three separate instants during the transit before the sight was lost in the sunset (see Figure 6).

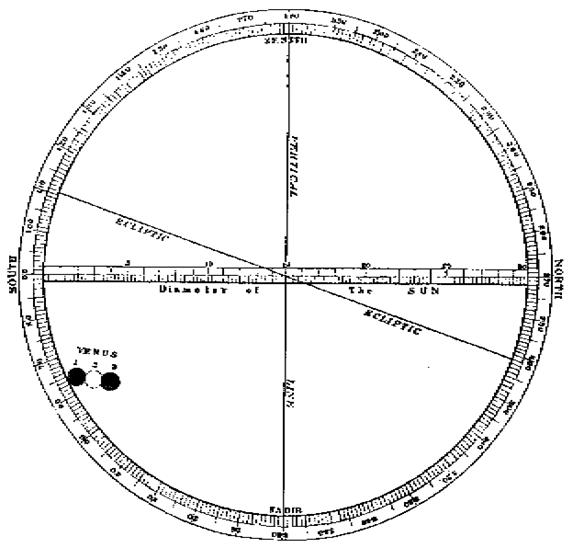
Figure 6: Horrocks' Observations of Venus in Transit

(from 'A Sourcebook in Astronomy', by H.Shapley & E.H.Howarth)

His measurements, expressed in a modernised form, were as shown on the following table:-

Local Apparent Time	Distance of Centres (as % of Sun's Diameter)
3.15 pm	48.06
3.35 pm	45.00
3.45 pm	43.33

The Sun's diameter for the transit day was estimated to be 31'30" and the diameter of Venus was estimated to be 4.0% of this (i.e. 1'16").

It seems that Horrocks ignored any correction for the flattening effect on the Sun's disk of refraction through the Earth's atmosphere. This effect would have been quite marked, given that all the measurements were taken within half-an-hour or so of sunset.

From extrapolation of his observations, Horrocks calculated the time of ingress and egress, the exact position of the node and the solar parallax - which he deduced was 14".

The method by which Horrocks' observations can be used to determine the solar parallax is outlined below. A simplifying assumption, that the orbits of Venus and the Earth are circular, is made. This means that we arrive at a slightly different answer from Horrocks.

In Figure 7 below, the distance from the Earth to Venus is EV, from the Sun to Venus is SV and, of course EV+ SV = 1 Astronomical Unit (AU).

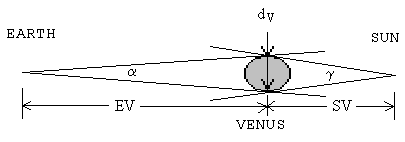
Figure 7: The Relationship between the Angles Subtended by Venus and its Distance from the Sun

In the above diagram, EV + SV = 1 (in astronomical units)

the diameter of Venus, dV = α EV = γ SV

therefore γ = α EV/SV = α ( 1 - SV )/SV

From Kepler's Third Law, the cube of the of a planet's orbital semi-major axis (in astronomical units) is equal to the square of the sidereal period (in Earth sidereal years) - i.e. in this case:-

SV³ = P_V²

SV = P_V

therefore, γ = α ( 1 -P_V² )/ P_V²

substituting, P_V = 0.6083 years and, α = 1'16"

γ = 30" (Horrocks value was approx 28")

Horrocks went on to assume, erroneously, that the Earth's diameter also subtended 28" at the centre of the Sun. Mercury and Mars had been shown to be of this order and he assumed that all planets would obey this rule. On the basis of this assumption, it can be seen from Figure 1 that the solar parallax would be 14" and the astronomical unit would be equal to rE/tan 14" - i.e. approximately 14,700 times the radius of the Earth.

Although Jeremiah Horrocks' assumption, that all the planets subtend the same angle at the Sun, was unfounded, it did come fairly close to the truth for the terrestrial planets. Consequently, his value for the astronomical unit was much more accurate than any calculated hitherto. It was also far greater than any previous values.

5. Predictions of Transits of Venus