Home Transit of Venus Sewer History
in Leeds Sundials in Leeds William
Gascoigne John Feild
About
Part 2 - The Distance to the Sun
From careful observation of the angle between the centres of the
Moon and the Sun at the waxing or waning Quarter Moon - i.e. when exactly half
of the Moons disk (as seen from the Earth) was in darkness - Aristarchus of
Samos (c.310 - 230 BC) arrived at relative distances for the Moon and the
Sun (see Figure 3). It is notoriously difficult to gauge exactly when
the Moon's shadow - the terminator - is at the half way point: after all the
Moon's surface is rough and the shadow does not follow a perfectly straight
line. Consequently, the angle measured by Aristarchus was quite inaccurate:
87°. Even so, the resulting ratio (1/cos 87°), showing that the Sun was about
20 times further away than the Moon, provided the first indication that the Sun
was an extraordinarily distant object.
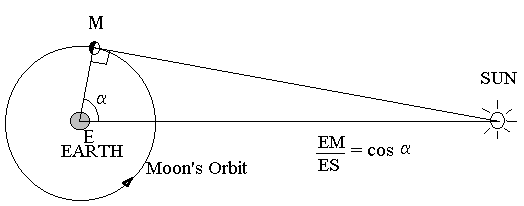
Figure
3: Aristarchus' Method for determining the relative distances of the Sun and
Moon
Estimates of the Solar Parallax made in antiquity, by astronomers
such as Aristarchus, Hipparchus (c.162 - c.126 BC) and Ptolemy
(c.140 AD) were still current in the Seventeenth Century. Even the great
observational astronomer, Tycho Brahe (1546 - 1601) accepted the
traditional value of 3'. In the years to follow however, estimates of this
angle decreased its magnitude drastically. Thus the Sun itself was judged to be
further and further from the Earth. The corollary to this was that the Sun was
becoming even more immense relative to the Earth. Johannes Kepler (1571-
1630) derived a Parallax of less than 1' from his observations of Mars. Around
1630, Vendelinus used a telescope and Aristarchus' method to obtain a
more accurate value for the ratio of the Earth-Sun distance and the Earth-Moon
distance. His ratio was about 229 (based on an angle of 89.75° ). This was much
closer to the modern value of 390.
The Orbits of the Inferior Planets
Relative distances of the inferior planets - Mercury and Venus -
compared with the distance to the Sun could be roughly deduced by measuring the
angle between the Sun and these planets at their greatest elongation. Nicholas
Copernicus (1473-1543) used this method to determine the relative radii of
the orbits of Venus and the Earth (see Figure 4). Observation of the
movement of Venus had the potential to yield a much richer harvest of
information however than had been imagined by Copernicus. In order to
understand how this is so, we need to consider in more detail the orbit of
Venus.
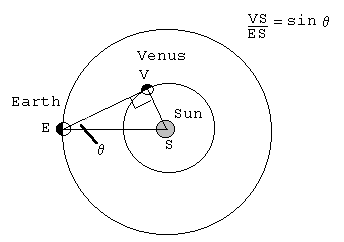
Figure
4: Venus at Greatest Elongation
The
orbits of Mercury and Venus do not lie in the ecliptic plane - i.e. the orbital
planes of these planets are at an angle to that of the Earth's orbit about the
Sun.
|
Inferior Planet |
Inclination of Orbit |
|
Mercury |
7.0° |
|
Venus |
3.4° |
When at inferior conjunction - i.e. when placed between the Earth
and the Sun - these planets do not necessarily lie on a straight line from the
Earth to the Sun. Only when the inferior conjunction happens to take place
virtually at the point where the planet's orbit crosses the Earth's orbital
plane will the planet be on such a straight line. During this kind of
conjunction the planet will appear to cross the Sun's disk. This is known as a
Transit of the planet.