Home Transit of Venus Sewer History
in Leeds Sundials in Leeds William
Gascoigne John Feild
About
Part 3 - Orbital Details of Venus
Transits of Venus are very rare - much rarer than transits of
Mercury.
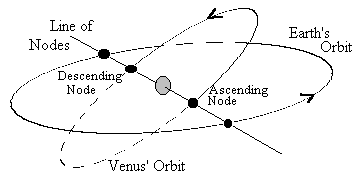
The points where the orbit of Venus (or any other planet) crosses
the Ecliptic are called the 'nodes'. The ascending node is where the
planet crosses from south to north; the descending node is where it
crosses from north to south.
The starting point for determining how frequently Venus will pass
through the ascending node of its orbit is to measure the synodic period
of the planet. The synodic period is the period taken between successive
appearances at the same point relative to the Sun as seen from the Earth.
In the case of Venus, the period between successive inferior
conjunctions - i.e. the synodic period - is 583.92 days.
The synodic period of Venus is more than one Earth year and less
than two Earth years. Therefore, we can conclude that the Earth has been
'lapped' once. Venus passes through the ascending node of its orbit however,
only when it reaches the same point in its orbit relative to a wider frame of
reference - i.e. relative to the stars. This period is known as the sidereal
period of Venus.
Synodic
Period of Venus, S=583.92 days
Sidereal
Period of Earth, E=365.256 days
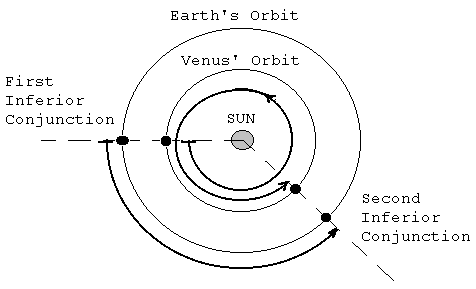
Figure
5: The relationship between the Synodic and Sidereal Periods of Venus
In relation to the above diagram, let S be the synodic period of
Venus, let P be its sidereal period and let E be the sidereal period of the
Earth, then:
S 2π
/P = S 2π
/E + 2π
(Note: see below for explanation)
Therefore, 1/P = 1/E + 1/S
Therefore, the Sidereal Period, P = 224.701 days
Thus, Venus completes one orbit around the Sun in much less time
than does the Earth
Note:
The rate of rotation of the Earth about the Sun = 2 π / E (radians/day)
The rate of rotation of Venus about the Sun = 2 π / P (radians/day)
The total angle moved by Venus in the synodic period, S, is
therefore = S.2 π
/ P
From figure 5 it can be seen that the angle moved Venus is equal
to one full orbit (2 p ) plus the total angle moved by the Earth (S.2 p / E) in
the same time
- i.e. ( S.2 π /
P ) =( S.2 π
/ E ) + 2 π