Home Transit of Venus Sewer History
in Leeds Sundials in Leeds William
Gascoigne John Feild
About
Part 6 - To the
During a stay on the
"We therefore recommend again and again, to the curious
investigators of the stars to whom, when our lives are over, these observations
are entrusted, that they, mindful of our advice, apply themselves to the
undertaking of these observations vigorously. And for them we desire and pray
for all good luck, especially that they be not deprived of this coveted spectacle
by the unfortunate obscuration of cloudy heavens, and that the immensities of
the celestial spheres, compelled to more precise boundaries, may at last yield
to their glory and eternal fame."
Halley prophesied that his paper would be "immortal", and
indeed it was. His exhortations and detailed plans, projected beyond the grave,
caused well-equipped expeditions to set out to far flung corners of the Earth
to observe the 1761 and 1769 transits.
In 1761, Charles Mason and Jeremiah Dixon observed
from
Having got there eventually, he decided to stay 8 years to make
sure of seeing the 1769 transit. Tragically, he missed this one too, because in
an otherwise cloud-free month a cloudy morning managed to totally obscure the
transit. To add insult to injury, when he returned to
An even greater number of expeditions set out to monitor the 1769
transit. Amongst these was the famous voyage of Captain James Cook, which
set up an observing station in
A summary of the results of some of these expeditions is shown in Figure
10. As can be seen, the timings of ingress and egress permitted different
chords to be plotted.
From the perpendicular distance between these chords, relative to
the known angle subtended at the Earth by the diameter of the Sun, it is
possible to compute the solar parallax [2].
In Figure 11, D = d . Lv/(LE - Lv ) (from similar triangles)
the ratio Lv / LE however was known from Kepler's Third Law. In
cruder terms, it was equal to sin θ (where θ was the angle of
greatest eastern elongation of Venus - see Figure 4)
Therefore, D = d . sin θ. LE/(LE( 1 - sin θ)) = d . sin
θ/( 1 - sin θ)
Consequently, from the ratio D / H (based on Figure 10), H (the
diameter of the Sun) can be calculated and hence the solar parallax and the
distance to the Sun.
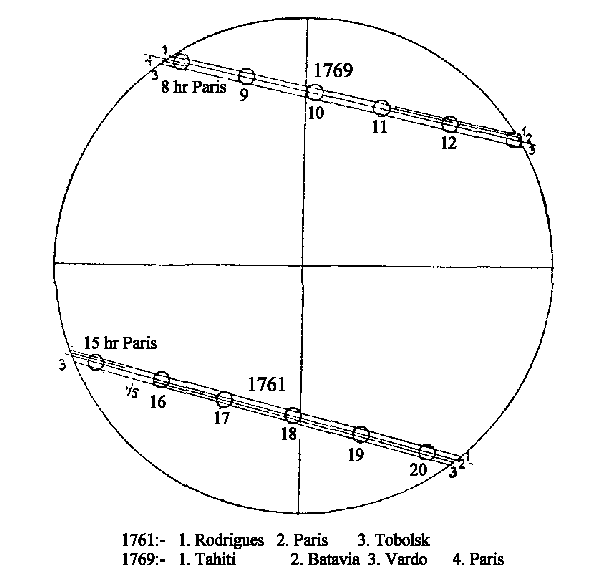
Figure
10: The Observed Tracks of Venus across the Face of the Sun during the Transits
of 1761 and 1769
Halley had pointed out that the duration of the transit of Venus
would be of the order of 7 hours. Venus would make approximately 1 arcsecond of
progress per 14 seconds of time (for a central transit, given that the angle
subtended by the Sun was about 31' 30" ). He reckoned that an error of 3
seconds in the measurement of time would produce only a 1% error in the
parallax.
The results were not as good as expected. It proved difficult to
discern exactly when the moments of contact took place (due to the 'black-drop'
effect) and also the longitude of some of the observing stations was not known
with sufficient accuracy. Nevertheless, the accuracy of the measurements
represented a great achievement.
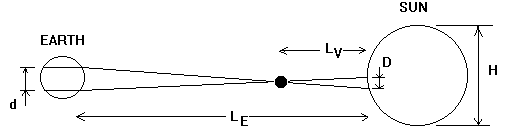
Figure
11: Halley's Method for computing the Solar Parallax
When
all the results were fed back, the calculated solar parallax varied between
8.55" and 8.88". The modern accepted value is 8.794148".
It can be truly said, that the real distance from the Earth to the
Sun - the 'Astronomical Unit' - was at last discovered. Kepler's laws had
already enabled the relative distances of the planets from the Sun (in
Astronomical Units) to be determined. Now - as a result of the selfless efforts
and dedication of numerous astronomers, explorers, surveyors and sailors - the absolute
dimensions of the Solar System could be fathomed.
Note [1]: Or, at least, so say some books!
This story is given by A.Pannekoek 'A History of Astronomy',
Note [2]: Please note that this simple explanation
is only intended to show that geometrical relationships exist which allow the
solar parallax to be determined by measuring durations of the Transit of Venus
at different locations. In practice, Halley's method of durations requires the
use of quite complex trigonometry. To see how exactly this is done, old
textbooks on spherical astronomy need to be consulted - e.g "A Treatise on
Spherical Astronomy" by R.S.Ball (1908,