![]() Home Transit of Venus Sewer
History in Leeds Sundials in Leeds William
Gascoigne John Feild About
Home Transit of Venus Sewer
History in Leeds Sundials in Leeds William
Gascoigne John Feild About
![]()
Part 8 - EDMOND HALLEY'S FAMOUS ADMONITION of 1716
PHILOSOPHICAL TRANSACTIONS VOL. XXIX (1716) A new Method of
determining the Parallax of the Sun, or his Distance from the Earth; by Dr.
Halley, Sec. R. S. N0 348, p.454. Translated from the Latin.
It is well known that this distance of the sun from the earth, is
supposed different by different astronomers. Ptolemy and his followers, as also
Coper-nicus and Tycho Brahe, have computed it at 1200 semi-diameters of the
earth, and Kepler at almost 3500; Riccioli doubles this last distance, and
Hevelius makes it only half as much. But at length it was found, on observing
by the telescope, Venus and Mercury on the sun's disk, divested of their
borrowed light, that the apparent diameters of the planets were much less than
hitherto they had been supposed to be; and in particular, that Venus's
semi-diameter, seen from the sun, only subtends the fourth part of a minute, or
15 seconds; and that Mercury's sem-diameter, at his mean distance from the sun,
is seen under an angle of 10 seconds only, and Saturn's semi-diameter under the
same angle; and that the semi-diameter of Jupiter, the largest of all the
planets, subtends no more than the third part of a minute at the sun. Whence,
by analogy, some modern astronomers conclude that the earth's semi-diameter,
seen from the sun, subtends a mean angle, between the greater of Jupiter and
the less of Saturn and Mercury, and equal to that of Venus, viz. one of 15
seconds; and consequently, that the distance of the sun from the earth is
almost 14,000 semi-diameters of the latter. Another consideration has made
these authors enlarge this distance a little more: for since the moon's
diameter is rather more than a quarter of the earth's diameter, if the sun's
parallax be supposed 15 seconds, the body of the moon would be larger than that
of Mercury, viz. a secondary planet larger than a primary one, which seems
repugnant to the regular proportion and symmetry of the mundane system. On the
contrary, it seems hardly consistent with the same proportion, that Venus, an
inferior planet, and without any satellite, should be larger than our earth, a
superior planet, and accompanied with so remarkable a satellite. Therefore, at
a mean, supposing the earth's semi-diameter, seen from the sun, or which is the
same thing, the sun's horizontal parallax, to be 12 seconds and a half, the
moon will be less than Mercury, and the earth larger than Venus, and the sun's
distance from the earth come out nearly 16500 semi-diameters of the earth. I
shall admit of this distance at present, till its precise quantity be made to
appear more certain by the trial I propose; not regarding the authority of such
as set the sun at an immensely greater distance, relying on the observa-tions
of a vibrating pendulum, which do not seem accurate enough to deter-mine such
minute angles; at least, such as use this method will find the parallax
sometimes none at all, and sometimes even negative; that is, the distance will
become either infinite, or more than infinite, which is absurd. And it is
scarcely possible for any one certainly to determine, by means of in-struments,
however nice, single seconds, or even 10 seconds; and therefore, it is not at
all surprising, that the exceeding minuteness of such angles has hitherto
baffled the many and ingenious attempts of artists.
While I was making my observations in the island of St. Helena,
about 40 years since, on the stars round the south pole, I happened to observe,
with the utmost care, Mercury passing over the sun's disk: and contrary to
expectation, I very accurately obtained, with a good 24-foot telescope, the
very moment in which Mercury, entering the sun's limb, seemed to touch it
internally, as also that of his going off; forming an angle of internal
contact. Hence I discovered the precise quantity of time the whole body of
Mercury had then appeared within the sun's disk, and that without an error of
one single second of time; for, the thread of solar light, intercepted between
the obscure limb of the planet, and the bright limb of the sun, though
exceedingly slender, affected my sight, and in the twinkling of an eye, both
the indenture made on the sun's limb by Mercury entering into it, vanished, and
that made by his going off, appeared. On observing this I immediately
concluded, that the sun's parallax might be duly determined by such
observations, if Mercury, being nearer the earth, had a greater parallax, when
seen from the sun; for, this difference of parallaxes is so very
inconsiderable, as to be always less than the sun's parallax, which is sought;
consequently, though Mercury is to be frequently seen within the sun's disk; he
will scarcely be fit for the present purpose.
There remains therefore Venus's transit over the sun's disk, whose
parallax, being almost 4 times greater than that of the sun, will cause very
sensible differences between the times in which Venus shall seem to pass over
the sun's disk in different parts of our earth. From these differences, duly
observed, the sun's parallax may be determined, even to a small part of a
second of time; and that without any other instruments than telescopes and good
common clocks, and without any other qualifications in the observer than
fidelity and diligence, with a little skill in astronomy. For we need not be
scrupulous in finding the latitude of the place, or in accurately determining
the hours with respect to the meridian; it is sufficient, if the times be
reckoned by clocks, truly corrected according to the revolutions of the
heavens, from the total ingress of Venus on the sun's disk, to the beginning of
her egress from it, when her opaque globe begins to touch the bright limb of
the sun; which times, as I found by experience, may be observed even to a
single second of time.
But by the limited laws of motion, Venus is very rarely seen
within the sun's disk; and for a series of 120 years, and upwards, is not to be
seen there once; viz. from 1639, when Mr. Horrox was favoured with this
agreeable sight, and he the first and only one since the creation of the world,
down to 1761; at which time, according to the theories hitherto observed in the
heavens, Venus will pass over the sun on May 26 in the morning; so that (vide
Phil. Trans. N0 193) at London, nearly at 6 o'clock in the morning, she is to
be in the middle of the sun's disk, and but 4 minutes more southerly than his
centre. The duration of this transit will be almost 8 hours; viz. from 2 till
near 10 o'clock in the morning. Consequently her ingress will not be visible in
England: but the sun at that time being in 16° of Gemini, and almost in 23° of
north declination, will be seen not to set throughout the whole northern frigid
zone; and consequently the inhabitants of the coast of Norway, as far as its
northern promontory, beyond the town of Drontheim, may observe Venus entering
the sun's disk; and perhaps this ingress into the sun at his rising may be seen
by the inhabitants of the north of Scotland and those of Zetland. But when
Venus is nearest the sun's centre, he will be vertical to the northern coasts
of the gulph of Ganga, or rather of the kingdom of Pegu; and consequently, in
the neighbouring countries, when the sun shall, at the ingress of Venus, be
almost 4 hours distant to the east, and almost as many to the west at her
egress, her apparent motion within the sun's disk will be accelerated almost
twice as much as in the horizontal parallax of Venus from the sun; because
Venus at that time moves retrograde from east to west; while in the mean time
an eye, on the surface of the earth, is carried the contrary way, from west to
east.
Supposing the sun's parallax, as was said, to be 12 seconds and a
half, Venus's parallax will be 43 seconds; and subtracting the sun's parallax,
there will remain half a minute at least for the horizontal parallax of Venus
from the sun, and consequently, Venus's motion will be accelerated ¾ of a
minute at least by that parallax, while she passes over the sun's disk, in such
elevations of the pole as are near the Tropic; and still more so near the
equator. For Venus will at that time accurately enough describe within the
sun's disk 4 minutes an hour; and consequently, at least 11 minutes of time (by
which the duration of this eclipse of Venus will be contracted by reason of the
parallax) answer to ¾ of a minute. And by this contraction alone we might
safely determine the parallax, provided the sun's diameter and Venus's latitude
were very accurately given; which yet we cannot possibly bring to a
calculation, in a matter of such great subtlety.
We must therefore have another observation, if possible, in places
where Venus possesses the middle of the sun at midnight, viz. under the
opposite meridian, that is, 6h or 90° more westerly than London, and where
Venus enters the sun's disk a little before his setting, and goes off a little
after his rising; which will happen in the said meridian in about 56° of N.
lat. that is, at Nelson's harbour in Hudson's Bay. For, in the neighbouring
places Venus's parallax will protract the duration of the transit, and make it
at least 6 minutes longer; because while the sun seems to tend under the pole
from west to east, these places on the earth's surface will seem to be carried
with a contrary motion towards the west, that is, with a motion conspiring with
the proper motion of Venus; consequently Venus will seem to move slower within
the sun's disk, and continue longer on it.
If therefore in both places this transit happen to be duly
observed by proper persons, it is evident that the Mora will be longer by 17
entire minutes in Nelson's harbour, than in the East-Indies; nor does it matter
much whether the observation be made at Fort St. George, commonly called Maderas,
or at Bencoolen on the western coast of the island of Sumatra near the equator.
But if the French should incline to make the observation, Pondicherry on the
western coast of the gulph of Ganga, at the elevation of 12°, will be a proper
place for that purpose: and for the Dutch, their famous emporium Batavia is a
fit place. And indeed I would have several observations made of the same
phenomenon in different parts, both for further confirmation, and lest a single
observer should happen to be disappointed by the intervention of clouds from
seeing what I know not if those either of the present or following age shall
ever see again; and upon which, the certain and adequate solution of the
noblest, and otherwise most difficult problem depends. Therefore again and
again, I recommend it to the curious strenuously to apply themselves to this
observation.
By this means, the sun's parallax may be discovered, to within its
five hundredth part, which will doubtless seem surprising to some: but yet, if
an accurate observation be had in both the places above-mentioned, it has
already been shown that the duration of these eclipses of Venus differ from
each other by 17 entire minutes, on the supposition that the sun's parallax is
12½ seconds. And if this difference be found to be greater or less by
observation, the sun's parallax will be greater or less nearly in the same
ratio. And since 17 minutes of time answer to 12½ seconds of the sun's
parallax; for each second of the parallax there will arise a difference of
upwards of 80 seconds of time; therefore, if this difference be obtained true
within 2 seconds of time, the quantity of the sun's parallax will be got to
within the 40th part of one second; and consequently his distance will be
determined to within its 500th part; at least if the parallax be not found less
than what I have supposed it; for 40 x 12½ is 500.
Here I have had no regard to the planet's latitude, both to avoid
the trouble of a more intricate calculation, which would render the conclusion
less evident, as also on account of the motion of the nodes of Venus not being
hitherto discovered, and which can only be duly determined by such conjunctions
of the planet with the sun as this. For it was only on the supposition, that
the plane of Venus's orbit is immoveable in the sphere of the fixed stars, and
that her nodes would continue in the same places as they were in 1639, that it
was concluded, that Venus would pass 4 minutes below the sun's centre. But if
in 1761 she should pass more southerly, it will be evident, that there is a
regression of the nodes; and if more northerly, that there is a progression of
them; and that at the rate of 5½ minutes in 100 Julian years, for each minute
by which the path of Venus will at that time be more or less distant from the sun's
centre than the said 4 minutes. But the difference between the durations of
these eclipses will be somewhat less than 17 minutes, by reason of the southern
latitude of Venus; but greater if, by the progression of the nodes, she shall
pass over the sun to the north of his centre.
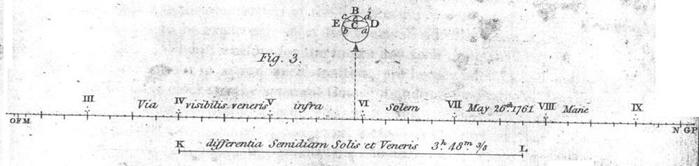
But for the sake of such as are not thoroughly acquainted with the
doctrine of parallaxes, I shall further explain the matter both by a figure and
a somewhat more accurate calculation. Therefore, supposing that at London, May
25, 17h55m, 1761, the sun be in 15° 37' of Gemini, and consequently that at his
centre the ecliptic tends towards the north in an angle of 6° 10'; and that the
visible path of Venus within the sun's disk at that time descends towards the
south, forming an angle with the ecliptic of 8° 28'; then the path of Venus
will tend a little towards the south in respect of the equator, intersecting
the parallels of declination in an angle of 2° 18'. Supposing likewise that
Venus be near the sun's centre at the said time, and distant from it towards
the south 4 minutes, describing, by a retrograde motion on the sun's disk, 4
minutes an hour. The sun's semi-diameter will be nearly 15' 51", and that
of Venus 37½". And supposing, for trial sake, the difference of the
horizontal parallaxes of Venus and the sun to be 31", such as it is on the
supposition of the sun's parallax being 12½". Therefore let a small
circle, as AEBD, fig. 3, pl. 5, be described from the centre C,
whose semi-diameter let be 31", representing the earth's disk, and in it
drawing DabE and cde the ellipses of the parallels of 22 and 56°
N. lat. in the same manner as is now used by astronomers for constructing solar
eclipses: and let BCA be the meridian in which the sun is, to which let
be inclined the right line FHG, representing the path of Venus, in an
angle of 2° 18', whose distance from the centre C let be 240 such parts
as BC is 31; and from C let fall the right line CH
perpendicular upon FG. Then supposing the planet in H at 17h55m,
or 5h55m in the morning, let the right line FHG be divided into the
horary spaces III; IV, IV; V, V; VI, &c. equal to CH, that is, 4
minutes. Let the right line KL be also equal to the difference of the
apparent semi-diameters of the sun and Venus, or 15' 13½". Then the
circle, described with the radius KL, and from any point within the
small circle, representing the earth's disk as a centre, will meet the right
line FG in the point denoting what o'clock it is at London, when Venus
shall touch the sun's limb in an angle of internal contact, in that place of
the earth's superficies that lies under the assumed point on the disk. And if a
circle, described from the centre C and with the radius KL, meet FG
in the points F and G, the right lines FH, HG will
be = 14' 41", which Venus will appear to pass over in 3h40m. Therefore F
will fall upon 2h5m at London, and G upon 9h35m in the morning. Whence
it is evident, that if the earth's magnitude should vanish, as it were, into a
point, by reason of the immense distance; or if, divested of its diurnal
motion, it should always have the sun vertical to the same point C, the
entire mora of this eclipse would continue for 7¾ hours. But in the mean time
while the earth revolves with a contrary motion to that of Venus through 110°
of long. and consequently the duration of the said mora is shorter, suppose by
12 minutes, it will be nearly 7h8m, or 107°.
Now in the meridian itself Venus will be near the sun's centre at
the eastern mouth of the Ganges, where the elevation of the pole is about 22°.
Therefore that place will be equally distant from the sun on both hands, in the
moments of the planet's ingress and egress, viz. 53½°; as the points a, b,
in the greater parallel DabE. But the diameter AB will be to the
distance ab, as the square of the radius to the rectangle under the
sines of 53½° and 68°, that is, as 1' 2" is to 46" 13"'; and on
making a due calculation, I find that the circle described with the radius KL,
from the centre a, will meet the right line FH in the point M,
at 2h20m40s; but described from the centre b, it will meet HG in N,
at 9h29m22s at London; consequently, the whole body of Venus will be seen the
banks of the Ganges, within the sun's disk, for 7h8m42s. Therefore we have
rightly supposed its duration 7h8m, since here a part of a minute is
inconsiderable.
But adapting the calculation to Nelson's harbour, I find that
Venus shall pass over the sun's disk, when he is just about to set, and emerge
out of his disk immediately after his rising, that place in the mean time being
carried through the hemisphere opposite to the sun from c to d,
with a motion conspiring with that of Venus. Therefore the mora of Venus within
the sun's disk will become longer by reason of the parallax, suppose by 4
minutes, so as entirely to be 7h24m or 111° of the equator. And since the
latitude of the place is 56°, it will be as the square of the radius is to the
rectangle under the sines of 55½° and 34°, so is AB = 1' 2" to cd
= 28" 33"'. And on duly making the calculation, it will appear, that
the circle, described from the centre c, with the radius KL, will
meet the right line FH in O, at 2h12m45s; but described from the
centre d, it will meet HG in P, at 9h36m37s. Therefore the
duration of the mora at Nelson's harbour will be 7h23m52s, viz. greater than at
the mouth of the Ganges by 15ml0s of time. But if Venus should pass without
latitude, the said difference will become 18m40s; and if she shall be 4 minutes
more northerly than the sun's centre, the difference will be increased to
21m40s, and will be still greater by increasing the planet's N. lat.
From the above hypothesis it follows, that at London Venus will
rise when entered into the sun, and at 9h37m in the morning in her egress touch
internally the sun's limb, and quite leave his disk not before 9h56m.
It is evident from the same hypothesis, that Venus should touch
with her centre the extreme northern limb of the sun on May 23, 11h, 1769, so
that, by reason of the parallax, her whole body may be seen in the northern
parts of Norway, within the sun's disk; while on the coast of Peru and Chili
she will seem to ride on the disk of the setting sun with a small segment of
her body; as in like manner in the Molucca islands, and the neighbouring parts,
at sun-rising. But if the nodes of Venus be found to have a retrocession, as
there is reason to suspect from some later observations, then her whole body
being every where seen within the sun's disk, the greatest differences of these
eclipses will afford a still more evident proof of the sun's parallax.*
* The transit of Venus in 1761 proved much less favourable to
the proposed purpose than Dr. Halley expected. The motion of Venus's node not
being well known, she passed much nearer the sun's centre than he supposed she
would; which made the places he pointed out for observing the total duration
not proper for the purpose; indeed the entrance of Venus on the sun could not
be seen at Hudson's Bay. He made a mistake too in the calculation, in taking
the sum instead of the difference, of the angle of the ecliptic with the
parallel to the equator, and the angle of Venus's path.
This translation of Halley's paper is
taken from the Abridged Transactions of the Royal Society, Volume VI,
pp.243-249, published in 1809.