Home Transit of Venus Sewer History in Leeds Sundials in Leeds William Gascoigne John Feild About

THE TRANSIT OF VENUS

& The Quest for the Solar Parallax

by David Sellers (Leeds, UK)

Almost every High School child knows that the Sun is 93 million miles (or 150 million Kilometres) away from the Earth. Despite the incredible immensity of this figure in comparison with everyday scales - or perhaps even because it is so hard to grasp - astronomical data of this kind is accepted on trust by most educated people. Very few pause to consider how it could be possible to measure such a distance - the 'Astronomical Unit' - and few are aware of the heroic efforts which attended early attempts at measuring it. Unfortunately, even most popular astronomy text books give insufficient information to allow one to see precisely how the task was accomplished.

Sizing the Yardstick: the Diameter of the Earth

In the history of astronomy, the quest for the Astronomical Unit (AU) has normally been regarded as the quest for a more fundamental quantity: namely, the 'Solar Parallax'. The solar parallax is not a distance at all. It is an angle: the angle subtended at the centre of the Sun by the Earth's radius (see Figure 1). If this angle is known and the radius of the Earth can be measured, then the distance to the Sun can be deduced by simple calculation. Clearly, the first piece of information which was needed in order to size the AU was the radius of the Earth.

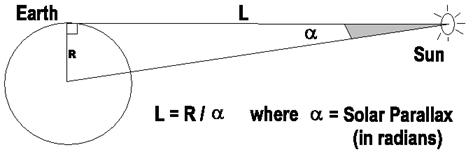
Figure 1: The Solar Parallax

The Greek astronomer, Eratosthenes of Cyrene (c276 - 195 BC), was able to deduce the Earth's radius by means of a strikingly simple set of observations. Eratosthenes found out that in the southern Egyptian town of Syene the Sun illuminated the bottom of a deep vertical well on the longest day of the year - i.e. when the Sun was at the Summer Sostice (see Figure 2). In Alexandria to the north however, at the same time, the shadow cast on a sundial was displaced from the vertical by an angle equal to 1/50 of a complete circumference (approximately 7°). Thus, concluded Eratosthenes, the surface distance between Syene and Alexandria must be 1/50 of the Earth's circumference. From the time taken for messengers to run between the towns, he estimated that their separation was 5000 stadia. Therefore the Earth's circumference must be 250,000 stadia. Unfortunately, no-one knows for certain what the modern equivalent to this unit is, but it seems probable that Eratosthenes obtained a reasonable value for the Earth's radius using this method. In Figure 2 it can be seen that, if the distance to the Sun is very much greater than the radius of the Earth, then angle OAZ is virtually equal to angle SCA. Thus:-

L / 2π R = γ / 2π Therefore, R = L / γ

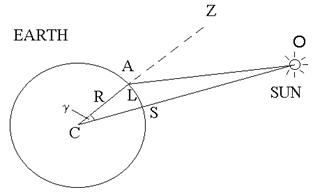
Figure 2: Eratosthenes Method for Deducing the Radius of the Earth

2. The Distance to the Sun